opengl之六 变换 Transformations
向量
向量最基本的定义就是一个方向。或者更正式的说,向量有一个方向(Direction)和大小(Magnitude,也叫做强度或长度)。
每个向量在2D图像中都用一个箭头(x, y)表示。由于向量表示的是方向,起始于何处并不会改变它的值。
向量与标量运算
标量(Scalar)只是一个数字(或者说是仅有一个分量的向量)。当把一个向量加/减/乘/除一个标量,可以简单的把向量的每个分量分别进行该运算。
其中的+可以是+,-,·或÷,其中·是乘号。注意-和÷运算时不能颠倒(标量-/÷向量),因为颠倒的运算是没有定义的。
向量取反
对一个向量取反(Negate)会将其方向逆转。在一个向量的每个分量前加负号就可以实现取反了(或者说用-1数乘该向量)。
向量加减
向量的加法可以被定义为是分量的(Component-wise)相加,即将一个向量中的每一个分量加上另一个向量的对应分量
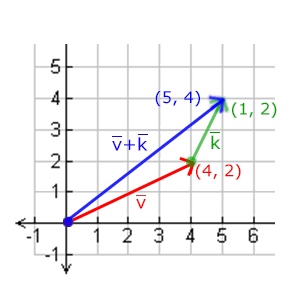
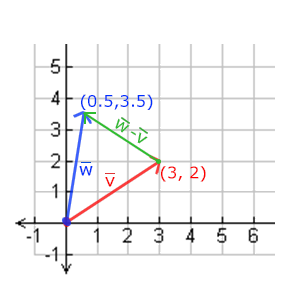
向量的减法等于加上第二个向量的相反向量。两个向量的相减会得到这两个向量指向位置的差。
长度
使用勾股定理(Pythagoras Theorem)来获取向量的长度(Length)/大小(Magnitude)。如果你把向量的x与y分量画出来,该向量会和x与y分量为边形成一个三角形:
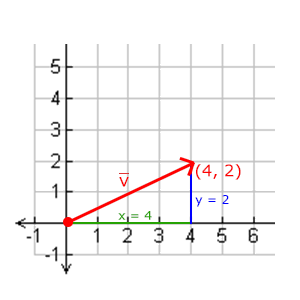
有一个特殊类型的向量叫做单位向量(Unit Vector)。单位向量有一个特别的性质——它的长度是1。可以用任意向量的每个分量除以向量的长度得到它的单位向量,这种方法叫做一个向量的标准化(Normalizing)。单位向量头上有一个^样子的记号。
向量相乘
向量相乘有两种,一种是点乘,另一种是叉乘。
点乘
两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值。
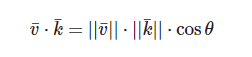
可以通过点乘的结果计算两个非单位向量的夹角,点乘的结果除以两个向量的长度之积,得到的结果就是夹角的余弦值
叉乘
叉乘只在3D空间中有定义,它需要两个不平行向量作为输入,生成一个正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的,那么叉乘之后将会产生3个互相正交的向量。
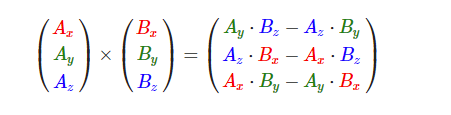
矩阵
简单来说矩阵就是一个矩形的数字、符号或表达式数组。矩阵中每一项叫做矩阵的元素(Element)
矩阵可以通过(i, j)进行索引,i是行,j是列。
矩阵的加减
矩阵与矩阵之间的加减就是两个矩阵对应元素的加减运算,所以总体的规则和与标量运算是差不多的,只不过在相同索引下的元素才能进行运算。这也就是说加法和减法只对同维度的矩阵才是有定义的。
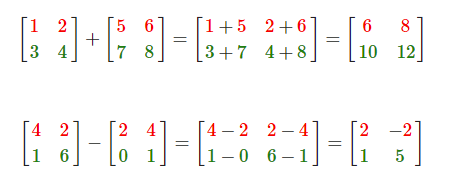
矩阵的数乘
和矩阵与标量的加减一样,矩阵与标量之间的乘法也是矩阵的每一个元素分别乘以该标量
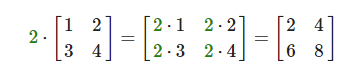
矩阵相乘
矩阵乘法基本上意味着遵照规定好的法则进行相乘。当然,相乘还有一些限制:
- 只有当左侧矩阵的列数与右侧矩阵的行数相等,两个矩阵才能相乘。
- 矩阵相乘不遵守交换律(Commutative),也就是说A⋅B≠B⋅A。

这些挑出来行和列将决定该计算结果2x2矩阵的哪个输出值。如果取的是左矩阵的第一行,输出值就会出现在结果矩阵的第一行。接下来再取一列,如果我们取的是右矩阵的第一列,最终值则会出现在结果矩阵的第一列。这正是红框里的情况。
计算一项的结果值的方式是先计算左侧矩阵对应行和右侧矩阵对应列的第一个元素之积,然后是第二个,第三个,第四个等等,然后把所有的乘积相加,这就是结果了。
结果矩阵的维度是(n, m),n等于左侧矩阵的行数,m等于右侧矩阵的列数。
矩阵与向量相乘
单位矩阵
单位矩阵是一个除了对角线以外都是0的N×N矩阵。
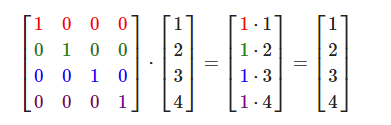
从乘法法则来看就很容易理解来:第一个结果元素是矩阵的第一行的每个元素乘以向量的每个对应元素。因为每行的元素除了第一个都是0,可得:1⋅1+0⋅2+0⋅3+0⋅4=1,向量的其他3个元素同理。
缩放
对一个向量进行缩放(Scaling)就是对向量的长度进行缩放,而保持它的方向不变。
如果每个轴的缩放因子都一样那么就叫均匀缩放(Uniform Scale)。
如果把缩放变量表示为(S1,S2,S3)可以为任意向量(x,y,z)定义一个缩放矩阵:
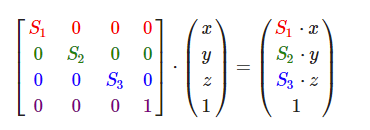
注意,第四个缩放向量仍然是1,因为在3D空间中缩放w分量是无意义的。w分量另有其他用途,
位移
位移(Translation)是在原始向量的基础上加上另一个向量从而获得一个在不同位置的新向量的过程,从而在位移向量基础上移动了原始向量。
和缩放矩阵一样,在4×4矩阵上有几个特别的位置用来执行特定的操作,对于位移来说它们是第四列最上面的3个值。如果我们把位移向量表示为(Tx,Ty,Tz),我们就能把位移矩阵定义为:
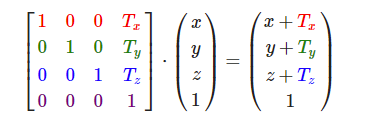
这样是能工作的,因为所有的位移值都要乘以向量的w行,所以位移值会加到向量的原始值上
有了位移矩阵就可以在3个方向(x、y、z)上移动物体,它是变换工具箱中非常有用的一个变换矩阵。
旋转
2D或3D空间中的旋转用角(Angle)来表示。角可以是角度制或弧度制的,周角是360角度或2 PI弧度
大多数旋转函数需要用弧度制的角,但幸运的是角度制的角也可以很容易地转化为弧度制的: 弧度转角度:角度 = 弧度 * (180.0f / PI) 角度转弧度:弧度 = 角度 * (PI / 180.0f) PI约等于3.14159265359
转半圈会旋转360/2 = 180度,向右旋转1/5圈表示向右旋转360/5 = 72度。
在3D空间中旋转需要定义一个角和一个旋转轴(Rotation Axis)。物体会沿着给定的旋转轴旋转特定角度。
当2D向量在3D空间中旋转时,把旋转轴设为z轴(尝试想象这种情况)。
旋转矩阵在3D空间中每个单位轴都有不同定义,旋转角度用θ表示:

利用旋转矩阵可以把任意位置向量沿一个单位旋转轴进行旋转。
其中(Rx,Ry,Rz)代表任意旋转轴:
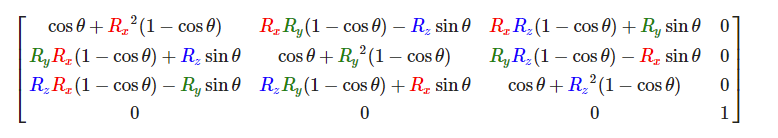
矩阵的组合
使用矩阵进行变换的真正力量在于,根据矩阵之间的乘法,可以把多个变换组合到一个矩阵中。
当矩阵相乘时,在最右边的矩阵是第一个与向量相乘的,所以你应该从右向左读这个乘法。 建议在组合矩阵时,先进行缩放操作,然后是旋转,最后才是位移,否则它们会(消极地)互相影响。
实践
GLM
GLM是OpenGL Mathematics的缩写,它是一个只有头文件的库,也就是说只需包含对应的头文件就行了,不用链接和编译。
GLM可以在这里下载,把头文件的根目录复制到你的includes文件夹,然后就可以使用这个库了。
GLM库从0.9.9版本起,默认会将矩阵类型初始化为一个零矩阵(所有元素均为0),而不是单位矩阵(对角元素为1,其它元素为0)。如果你使用的是0.9.9或0.9.9以上的版本,你需要将所有的矩阵初始化改为 glm::mat4 mat = glm::mat4(1.0f)。
大部分glm功能可以从下面3个头文件中找到:
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>
把一个向量(1, 0, 0)位移(1, 1, 0)个单位
glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
// 译注:下面就是矩阵初始化的一个例子,如果使用的是0.9.9及以上版本
// 下面这行代码就需要改为:
// glm::mat4 trans = glm::mat4(1.0f)
// 之后将不再进行提示
glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;
把单位矩阵和一个位移向量传递给glm::translate函数来完成这个工作的
下面例子逆时针旋转90度。然后缩放0.5倍,使它变成原来的一半大。
glm::mat4 trans;
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));
首先,在每个轴都缩放到0.5倍,然后沿z轴旋转90度。GLM希望它的角度是弧度制的(Radian),所以使用glm::radians将角度转化为弧度。注意有纹理的那面矩形是在XY平面上的,所以需要把它绕着z轴旋转。
如何把矩阵传递给着色器?
将修改顶点着色器让其接收一个mat4的uniform变量,然后再用矩阵uniform乘以位置向量:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;
out vec2 TexCoord;
uniform mat4 transform;
void main()
{
gl_Position = transform * vec4(aPos, 1.0f);
TexCoord = vec2(aTexCoord.x, 1.0 - aTexCoord.y);
}
在把位置向量传给gl_Position之前,先添加一个uniform,并且将其与变换矩阵相乘。
把变换矩阵传递给着色器
unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));
首先查询uniform变量的地址,然后用有Matrix4fv后缀的glUniform函数把矩阵数据发送给着色器
- 第一个参数是uniform的位置值
- 第二个参数告诉opengl将要发送多少个矩阵
- 第三个参数是否对矩阵进行置换,即交换矩阵行和列,GLM的默认布局就是列主序,所以并不需要置换矩阵,填GL_FALSE
- 最后一个参数是真正的矩阵数据,要先用GLM的自带的函数value_ptr来变换这些数据。