opengl光照之五 投光物 Light Casters
平行光
使用一个假设光源处于无限远处的模型时,它就被称为定向光,因为它的所有光线都有着相同的方向,它与光源的位置是没有关系的。
因为所有的光线都是平行的,所以物体与光源的相对位置是不重要的,因为对场景中每一个物体光的方向都是一致的。由于光的位置向量保持一致,场景中每个物体的光照计算将会是类似的。
struct Light {
// vec3 position; // 使用定向光就不再需要了
vec3 direction;
vec3 ambient;
vec3 diffuse;
vec3 specular;
};
...
void main()
{
vec3 lightDir = normalize(-light.direction);
...
}
首先对light.direction向量取反。目前使用的光照计算需求一个从片段至光源的光线方向,但人们更习惯定义定向光为一个从光源出发的全局方向。所以需要对全局光照方向向量取反来改变它的方向,它现在是一个指向光源的方向向量了。而且,记得对向量进行标准化,假设输入向量为一个单位向量是很不明智的。
最终的lightDir向量将和以前一样用在漫反射和镜面光计算中。
先定义了十个不同的箱子位置,并对每个箱子都生成了一个不同的模型矩阵,每个模型矩阵都包含了对应的局部-世界坐标变换:
glm::vec3 cubePositions[] = {
glm::vec3( 0.0f, 0.0f, 0.0f),
glm::vec3( 2.0f, 5.0f, -15.0f),
glm::vec3(-1.5f, -2.2f, -2.5f),
glm::vec3(-3.8f, -2.0f, -12.3f),
glm::vec3( 2.4f, -0.4f, -3.5f),
glm::vec3(-1.7f, 3.0f, -7.5f),
glm::vec3( 1.3f, -2.0f, -2.5f),
glm::vec3( 1.5f, 2.0f, -2.5f),
glm::vec3( 1.5f, 0.2f, -1.5f),
glm::vec3(-1.3f, 1.0f, -1.5f)
};
for(unsigned int i = 0; i < 10; i++)
{
glm::mat4 model;
model = glm::translate(model, cubePositions[i]);
float angle = 20.0f * i;
model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
lightingShader.setMat4("model", model);
glDrawArrays(GL_TRIANGLES, 0, 36);
}
不要忘记定义光源的方向(注意将方向定义为从光源出发的方向,你可以很容易看到光的方向朝下)。
lightingShader.setVec3("light.direction", -0.2f, -1.0f, -0.3f);
点光源
衰减
随着光线传播距离的增长逐渐削减光的强度通常叫做衰减(Attenuation)。随距离减少光强度的一种方式是使用一个线性方程。这样的方程能够随着距离的增长线性地减少光的强度,从而让远处的物体更暗。然而,这样的线性方程通常会看起来比较假。在现实世界中,灯在近处通常会非常亮,但随着距离的增加光源的亮度一开始会下降非常快,但在远处时剩余的光强度就会下降的非常缓慢了。所以,需要一个不同的公式来减少光的强度。
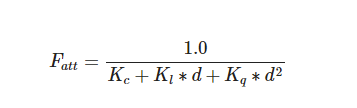
在这里d代表了片段距光源的距离。接下来为了计算衰减值,定义3个(可配置的)项:常数项Kc、一次项Kl和二次项Kq。
- 常数项通常保持为1.0,它的主要作用是保证分母永远不会比1小,否则的话在某些距离上它反而会增加强度,这肯定不是想要的效果。
- 一次项会与距离值相乘,以线性的方式减少强度。
- 二次项会与距离的平方相乘,让光源以二次递减的方式减少强度。二次项在距离比较小的时候影响会比一次项小很多,但当距离值比较大的时候它就会比一次项更大了。
由于二次项的存在,光线会在大部分时候以线性的方式衰退,直到距离变得足够大,让二次项超过一次项,光的强度会以更快的速度下降。这样的结果就是,光在近距离时亮度很高,但随着距离变远亮度迅速降低,最后会以更慢的速度减少亮度。
选择正确的值
| 距离 | 常数项 | 一次项 | 二次项 |
|---|---|---|---|
| 7 | 1.0 | 0.7 | 1.8 |
| 13 | 1.0 | 0.35 | 0.44 |
| 20 | 1.0 | 0.22 | 0.20 |
| 32 | 1.0 | 0.14 | 0.07 |
| 50 | 1.0 | 0.09 | 0.032 |
| 65 | 1.0 | 0.07 | 0.017 |
| 100 | 1.0 | 0.045 | 0.0075 |
| 160 | 1.0 | 0.027 | 0.0028 |
| 200 | 1.0 | 0.022 | 0.0019 |
| 325 | 1.0 | 0.014 | 0.0007 |
| 600 | 1.0 | 0.007 | 0.0002 |
| 3250 | 1.0 | 0.0014 | 0.000007 |
你可以看到,常数项Kc在所有的情况下都是1.0。一次项Kl为了覆盖更远的距离通常都很小,二次项Kq甚至更小。尝试对这些值进行实验,看看它们在你的实现中有什么效果。在我们的环境中,32到100的距离对大多数的光源都足够了。
实现衰减
为了实现衰减,在片段着色器中还需要三个额外的值:也就是公式中的常数项、一次项和二次项。它们最好储存在之前定义的Light结构体中。
struct Light {
vec3 position;
vec3 ambient;
vec3 diffuse;
vec3 specular;
float constant;
float linear;
float quadratic;
};
将在OpenGL中设置这些项:我们希望光源能够覆盖50的距离,所以会使用表格中对应的常数项、一次项和二次项:
lightingShader.setFloat("light.constant", 1.0f);
lightingShader.setFloat("light.linear", 0.09f);
lightingShader.setFloat("light.quadratic", 0.032f);
在片段着色器中实现衰减还是比较直接的:根据公式计算衰减值,之后再分别乘以环境光、漫反射和镜面光分量。
需要公式中距光源的距离,可以通过获取片段和光源之间的向量差,并获取结果向量的长度作为距离项。可以使用GLSL内建的length函数来完成这一点:
float distance = length(light.position - FragPos);
float attenuation = 1.0 / (light.constant + light.linear * distance +
light.quadratic * (distance * distance));
接下来,将包含这个衰减值到光照计算中,将它分别乘以环境光、漫反射和镜面光颜色。
ambient *= attenuation;
diffuse *= attenuation;
specular *= attenuation;
完整代码:github.com/realjf/opengl/src/lighting/05
聚光
OpenGL中聚光是用一个世界空间位置、一个方向和一个切光角(Cutoff Angle)来表示的,切光角指定了聚光的半径(译注:是圆锥的半径不是距光源距离那个半径)。
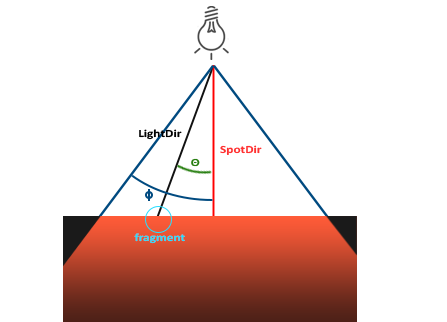
- LightDir:从片段指向光源的向量。
- SpotDir:聚光所指向的方向。
- Phiϕ:指定了聚光半径的切光角。落在这个角度之外的物体都不会被这个聚光所照亮。
- Thetaθ:LightDir向量和SpotDir向量之间的夹角。在聚光内部的话θ值应该比ϕ值小。
要做的就是计算LightDir向量和SpotDir向量之间的点积(还记得它会返回两个单位向量夹角的余弦值吗?),并将它与切光角ϕ值对比。
手电筒
手电筒(Flashlight)是一个位于观察者位置的聚光,通常它都会瞄准玩家视角的正前方。基本上说,手电筒就是普通的聚光,但它的位置和方向会随着玩家的位置和朝向不断更新。
所以,在片段着色器中需要的值有聚光的位置向量(来计算光的方向向量)、聚光的方向向量和一个切光角。我们可以将它们储存在Light结构体中:
struct Light {
vec3 position;
vec3 direction;
float cutOff;
...
};
接下来将合适的值传到着色器中:
lightingShader.setVec3("light.position", camera.Position);
lightingShader.setVec3("light.direction", camera.Front);
lightingShader.setFloat("light.cutOff", glm::cos(glm::radians(12.5f)));
并没有给切光角设置一个角度值,反而是用角度值计算了一个余弦值,将余弦结果传递到片段着色器中。这样做的原因是在片段着色器中,计算LightDir和SpotDir向量的点积,这个点积返回的将是一个余弦值而不是角度值,所以不能直接使用角度值和余弦值进行比较。为了获取角度值需要计算点积结果的反余弦,这是一个开销很大的计算。所以为了节约一点性能开销,计算切光角对应的余弦值,并将它的结果传入片段着色器中。由于这两个角度现在都由余弦角来表示了,可以直接对它们进行比较而不用进行任何开销高昂的计算。
接下来就是计算θ值,并将它和切光角ϕ对比,来决定是否在聚光的内部:
float theta = dot(lightDir, normalize(-light.direction));
if(theta > light.cutOff)
{
// 执行光照计算
}
else // 否则,使用环境光,让场景在聚光之外时不至于完全黑暗
color = vec4(light.ambient * vec3(texture(material.diffuse, TexCoords)), 1.0);
首先计算了lightDir和取反的direction向量(取反的是因为我们想让向量指向光源而不是从光源出发)之间的点积。记住要对所有的相关向量标准化。